频分复用

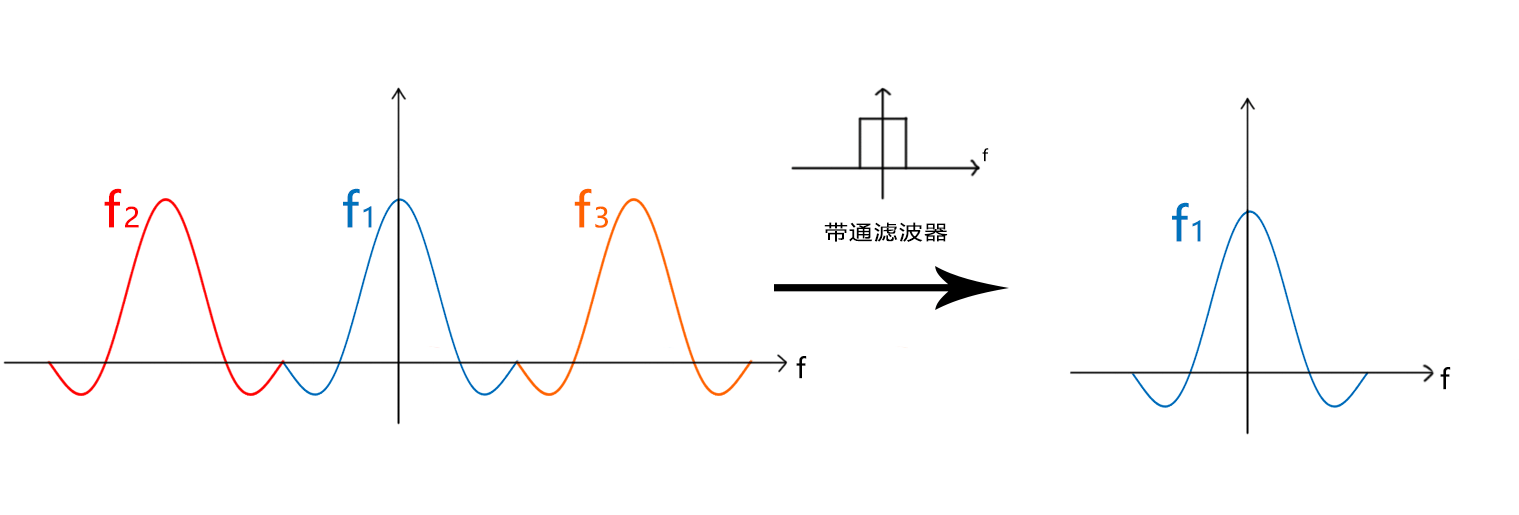
频分复用（FDM,Frequency Division Multiplexing）这个概念我们并不陌生。当用汽车接收广播的时候，每个电台节目使用不同的频率，就可以看成不同的载波。此时如果我们想听 f1 频道，那么经过与 f1 相一致的带通滤波器，这个电台节目就会被接收下来了。这是传统的FDM。

滤波示意图

但是频段资源是有限的，如果要支持成千上百的电台节目是很困难的，因此我们必须提高频段的利用率。

OFDM技术

单载波与多载波技术

单载波是指在一个固定的频段内只采用一个载波的调制技术，上面举的例子就是单载波的传输方案。单载波存在很多问题，除了频谱利用率低，还有之前所说的码间串扰 、回响、脉冲干扰、振幅不平衡、群延时响应等。

就码间串扰而言，单载波方法的码元速率相对较高，通常1MS/s～30MS/s，因此码元持续时间（符号速率的倒数）为1µs或更短。然而地面传输路径的反射波延迟很容易位于100µs～250µs范围内（大约70km），将导致相邻码元甚至更远距离码元的码间串扰。

显然为减少干扰：

  • 尽量延长符号持续时间；
  • 可以在符号间插入空白，叫做防护间隔（guard intervals）；
  • 同时在接收端，通过采用误码保护的方法恢复和重建信息。

如果信息不通过单一载波进行传输，而是分散到多个载波，最多成千个副载波，那么如果某个载波或载波带受到衰落影响，其余子载波不会受影响。同时，接收端可从相对不分散的载波中恢复出足够的无误码信息，并利用采取的误码保护措施来重建无误码的输出数据流。另外，如果采用成千的子载波使得符号速率将被降低，符号持续时间也将相应延长几千倍，最大到1ms。

这就是多载波传输的优势所在，那么我们的正交频分复用技术（OFDM,Orthogonal Frequency Division Multiplexing）是目前实现复杂度最低、应用最广的一种多载波传输方案。

多载波传输

三角函数的正交原理

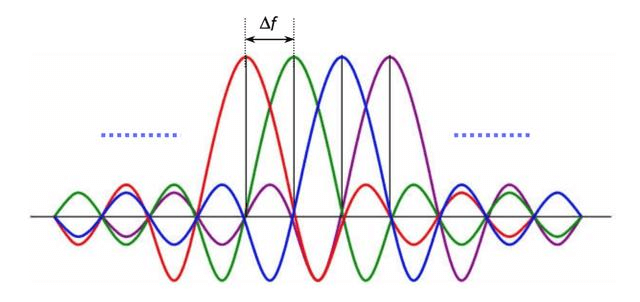
三角函数的正交原理是OFDM技术的最基本的原理，它是指不同频率的正弦波是正交的。下面我们来证明这一点。

假设有两个正弦波：sin⁡2πk1t\sin 2\pi k_{1} t 、sin⁡2πk2t\sin 2\pi k_{2} t，让我们来算一下二者在[0,1]区间内的积分 ∫01aksin⁡2πk1t⋅sin⁡2πk2tdt\int_{0}^{1} a_{k}\sin 2\pi k_{1} t \cdot \sin 2\pi k_{2} t \mathrm{d}t。

当k1=k2k_{1} = k_{2}时，

∫01aksin⁡(2πk1t)⋅sin⁡(2πk2t)dt=ak∫01sin⁡2(2πk1t)dt=ak∫011−cos⁡(4πk1t)2dt=ak2\begin{equation} \begin{split} \int_{0}^{1}a_{k} \sin( 2\pi k_{1}t ) \cdot \sin( 2\pi k_{2}t){d}t &= a_{k}\int_{0}^{1} \sin^{2} ( 2\pi k_{1} t ){d}t\\ &=a_{k}\int_{0}^{1} \frac{1-\cos(4\pi k_{1}t)}{2}{d}t\\ &=\frac{a_{k}}{2} \end{split} \end{equation}

当k1≠k2k_{1} \ne k_{2}时，

∫01aksin⁡(2πk1t)⋅sin⁡(2πk2t)dt=−ak2∫01[cos⁡（2πk1t+2πk2t）−cos⁡（2πk1t−2πk2t）]dt(设k1+k2=a,k1−k2=b)=−ak2∫01[cos⁡（2πat）−cos⁡（2πbt）]dt=0\begin{equation} \begin{split} \int_{0}^{1}a_{k} \sin( 2\pi k_{1} t )\cdot \sin( 2\pi k_{2} t) \mathrm{d}t &= - \frac{a_{k}}{2}\int_{0}^{1} [\cos（2\pi k_{1}t+2\pi k_{2}t）- \cos（2\pi k_{1}t-2\pi k_{2}t）] \mathrm{d}t\\&(设k_{1}+k_{2}=a,k_{1}-k_{2}=b)\\&=- \frac{a_{k}}{2}\int_{0}^{1} [\cos（2\pi at）- \cos（2\pi bt）] \mathrm{d}t\\&= 0 \end{split} \end{equation}

这表明这一系列不同频率的正弦函数是正交的。同理，余弦函数同样有此性质。这种数学上的性质，对于通信而言异常重要。

因为这些正弦函数就是通信中所说的子载波，aka_{k}就是我们要发送的信息，也就是一个码元，经过基带调制后，实际发送的信号为aksin⁡(2πkt)a_{k}\sin(2πkt)。

OFDM的调制与解调基本原理

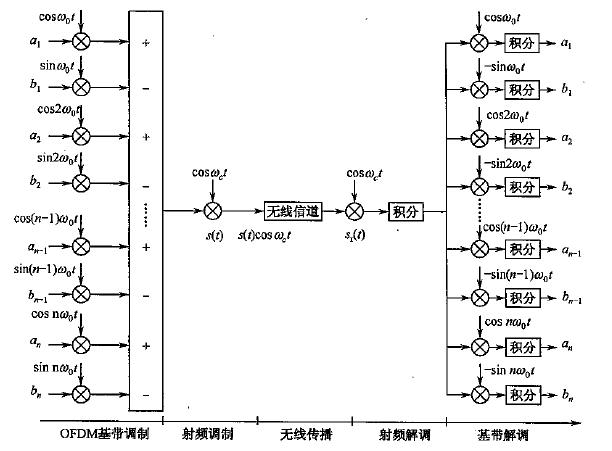
用原始要发送的信号aka_{k},bkb_{k}去调制相互正交的子载波序列 { sin⁡2πkt\sin2πkt,sin⁡2πkt\sin2πkt,sin⁡3πkt\sin3πkt } 和 { cos⁡2πkt\cos2πkt,cos⁡2πkt\cos2πkt,cos⁡3πkt\cos3πkt } ，然后进行累加，得到 s(t) ，这个 s(t) 是OFDM基带信号，是一个实信号，又由于基带信号的频率太低，不满足远距离传输的要求，那么经过射频调制后，就满足了。然后再用天线发射出去就可以了。

OFDM的调制与解调

解调所用的子载波与调制用的子载波同频同相，这是根据我们上面的推导（1）得出的，不管各子载波怎么杂糅，我们只要用哪一个子载波调制就用哪一个子载波解调，这样就可以得到我们想要的 aka_{k} 的信息。根据推导（2），子载波不相同的在同一码元周期内就会被积为0，因此毫无影响，这就是正交的好处。

参考资料